Formation Control

Many applications for cooperative multi-agent networks require the agents to arrange themselves into some spatial pattern. This can include alignment of orientations and velocities for flocking behaviors, or specific formations like spacecraft constellations for sensing or vehicle platoons for autonomous driving. The formation control problem seeks to design distributed control strategies for each agent that ensure the entire ensemble can arrange into the desired formation.

A fundamental challenge for solving the formation control problem relates to the sensing and control architecture for the multi-agent system. Our approach is to leverage results from rigidity theory. Rigidity theory studies the solution of a set of geometric constraints on a discrete configuration of points in an Euclidean space. These constraints can include distance or bearing constraints between pairs of points. Of interest in rigidity theory is to determine whether the set of polynomial equations representing these constraints (i) has a solution (independence); (ii) has locally isolated solutions (rigidity); or (iii) has exactly one solution in the given space up to isometric motions (global rigidity).

Our research explores various aspects of rigidity theory and formation control. Topics include:

  • Formation control using bearing sensing and bearing rigidity theory.
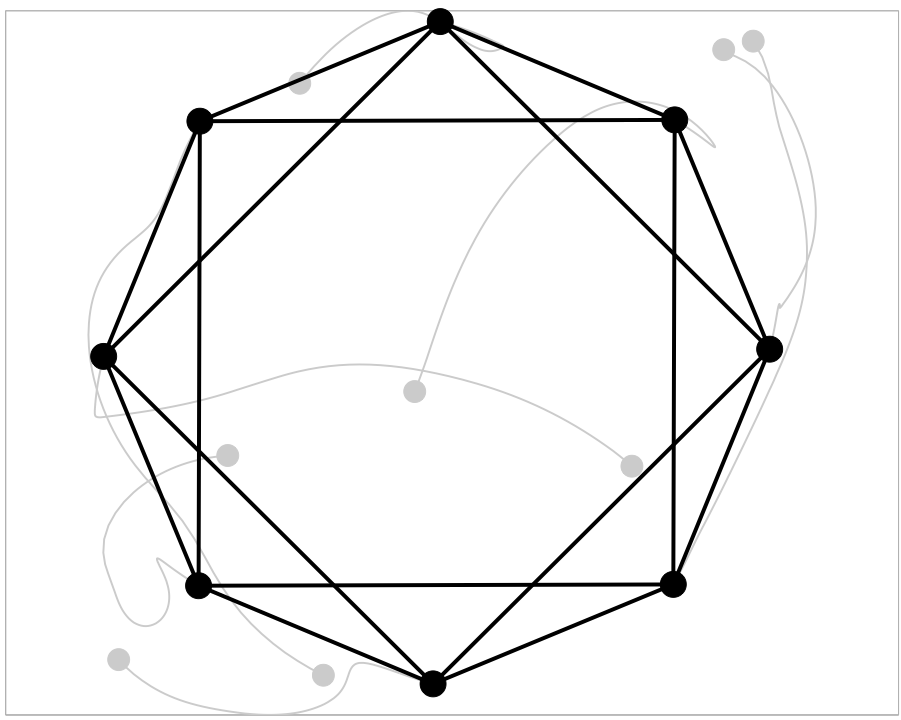
  • Alternative architectures exploiting symmetry found in formations.
  • Dynamic controllers to ensure the rigidity property is maintained in a multi-robot formation with uncertain environments.
  • Formations consisting of heterogeneous agent types with different sensing capabilities.
Bearing-only Formation Control Symmetry Forced Formations Formation Balancing

Related Publications:

  1. L. Theran, D. Zelazo, and J. Sidman, “A Geometric View of Formation Control with Application to Directed Sensing,” Dec. 2025.
    Theran_IFAC26.pdf arXiv: https://arxiv.org/abs/2512.06195 Theran_IFAC26.bibtex
  2. Z. Martinez and D. Zelazo, “Symmetry-Based Formation Control on Cycle Graphs Using Dihedral Point Groups,” Dec. 2025.
    Martinzez_IFAC26.pdf arXiv: https://arxiv.org/abs/2512.06733 Martinzez_IFAC26.bibtex
  3. S. Goldgraber Casspi and D. Zelazo, “The Geometry of Hidden Modes in Distance-Based Formation Control,” Nov. 2025.
    GoldgraberCasspi_IFAC26.pdf arXiv: https://arxiv.org/abs/2511.13187 GoldgraberCasspi_IFAC26.bibtex
  4. Z. Martinez and D. Zelazo, “Formation Control via Rotation Symmetry Constraints,” Oct. 2025.
    Martinez2026_ACC.pdf arXiv: https://arxiv.org/abs/2510.00676 Martinez2026_ACC.bibtex
  5. J. Shi and D. Zelazo, “Extending the Leader-First Follower Structure for Bearing-only Formation Control on Directed Graphs,” IEEE Transactions on Control of Network Systems, 1–12, 2025.
    Shi2025_TCNS.pdf DOI: 10.1109/TCNS.2025.3626655 Shi2025_TCNS.bibtex
  6. Z. Martinez, “Symmetry-Constrained Formation Maneuvering,” in IAAC Workshop: Graduate Students in Systems and Control, Haifa, Israel, Jul. 2025.
    Martinez_GSC2025.slides Martinez_GSC2025.bibtex
  7. D. Zelazo, S.-ichi Tanigawa, and B. Schulze, “Forced Symmetric Formation Control,” IEEE Transactions on Control of Network Systems, 12(2):1415–1426, 2025.
    zelazo2025TCNS.pdf DOI: 10.1109/TCNS.2025.3525814 zelazo2025TCNS.bibtex
  8. Z. Martinez and D. Zelazo, “Symmetry-Constrained Formation Maneuvering,” in 64th Israel Annual Conference on Aerospace Sciences, Haifa, Israel, Mar. 2025.
    Martinez2025_IACAS.pdf Martinez2025_IACAS.slides Martinez2025_IACAS.bibtex
  9. C. Xu, D. Zelazo, and B. Wu, “Distributed Prescribed-Time Coordinated Control of Spacecraft Formation Flying under Input Saturation,” Advances in Space Research, 74(5):2302–2315, 2024.
    Xu2023b_J.pdf DOI: https://doi.org/10.1016/j.asr.2024.05.077 Xu2023b_J.bibtex
  10. C. Xu, D. Zelazo, and B. Wu, “Bearing-based formation control of second-order multiagent systems with bounded disturbances,” International Journal on Robust and Nonlinear Control, 34(1):167–199, 2024.
    Xu2023a_J.pdf DOI: https://doi.org/10.1002/rnc.6966 Xu2023a_J.bibtex
  11. J. Shi and D. Zelazo, “Bearing-only Formation Control with Directed Sensing,” in 63rd Israel Annual Conference on Aerospace Sciences, Haifa, Israel, May 2024.
    Shi_IACAS2024.pdf Shi_IACAS2024.slides Shi_IACAS2024.bibtex
  12. M. Sewlia and D. Zelazo, “Bearing-Based Formation Stabilization Using Event-Triggered Control,” International Journal on Robust and Nonlinear Control, 34(6):4375–4387, 2024.
    Sewlia2023a_J.pdf DOI: 10.1002/rnc.7185 Sewlia2023a_J.bibtex
  13. J. Shi, “Bearing-only Formation Control with Directed Sensing,” mastersthesis, Technion - Israel Institute of Technology, Autonomous Systems and Robotics, 2024.
    Shi2024.pdf Shi2024.bibtex
  14. Z. Sun, S. Zhao, and D. Zelazo, “Characterizing bearing persistence in directed graphs,” in IFAC World Congress, Yokohama, Japan, Jul. 2023.
    Sun2023a_C.pdf DOI: 10.1016/j.ifacol.2023.10.1307 Sun2023a_C.poster Sun2023a_C.bibtex
  15. D. Zelazo, B. Shulze, and S.-I. Tanigawa, “Stabilization of Symmetric Formations,” in IFAC World Congress, Yokohama, Japan, Jul. 2023.
    Zelazo2023a_C.pdf Zelazo2023a_C.slides DOI: 10.1016/j.ifacol.2023.10.301 Zelazo2023a_C.bibtex
  16. M. Fabris and D. Zelazo, “Bearing-based Autonomous Communication Relay Positioning under Field-of-View Constraints,” Advanced Control for Applications, 4(2):e103, 2022.
    Fabris2021b_J.pdf DOI: 10.1002/adc2.103 Fabris2021b_J.bibtex
  17. B. Pozzan, G. Michieletto, A. Cenedese, and D. Zelazo, “Heterogeneous Formation Control: a Bearing Rigidity Approach,” in IEEE Conference on Decision and Control, Austin, Texas, Dec. 2021.
    Pozzan2021a.pdf DOI: 10.1109/cdc45484.2021.9683374 Pozzan2021a.bibtex
  18. G. Michieletto, A. Cenedese, and D. Zelazo, “A Unified Dissertation on Bearing Rigidity Theory,” IEEE Transactions on Control of Network Systems, 8(4):1624–1636, 2021.
    Michieletto2021_J.pdf DOI: 10.1109/TCNS.2021.3077712 Michieletto2021_J.bibtex
  19. M. H. Trinh, D. Zelazo, and H.-S. Ahn, “Pointing Consensus and Bearing-Based Solutions to the Fermat–Weber Location Problem,” IEEE Transactions on Automatic Control, 65(6):2339–2354, 2020.
    Trinh_TAC2020.pdf DOI: 10.1109/TAC.2019.2927932 Trinh_TAC2020.bibtex
  20. M. Sewlia, “Distributed Event-Triggered Control for Multi-Agent Systems with Second-Order Dynamics,” mastersthesis, Technion - Israel Institute of Technology, Aerospace Engineering Department, 2020.
    Sewlia2020.pdf Sewlia2020.bibtex
  21. T. Ikeda, D. Zelazo, and K. Kashima, “Maximum Hands-Off Distributed Bearing-Based Formation Control,” in IEEE Conference on Decision and Control, Nice, France, Dec. 2019.
    Ikeda2019a.pdf DOI: 10.1109/cdc40024.2019.9029574 Ikeda2019a.bibtex
  22. D. Zelazo and S. Zhao, “Formation Control and Rigidity Theory,” Snapshots of Modern Mathematics from Oberwolfach, (12):1–16, 2019.
    Zelazo2019a_J.pdf DOI: 10.14760/SNAP-2019-017-EN Zelazo2019a_J.bibtex
  23. A. Jain and D. Zelazo, “Temporal Circular Formation Control with Bounded Trajectories in a Uniform Flowfield,” in 27th Mediterranean Conference on Control and Automation, Akko, Israel, Jul. 2019.
    Jain2019a.pdf Jain2019a.slides DOI: 10.1109/med.2019.8798531 Jain2019a.bibtex
  24. Q. Van Tran, M. H. Trinh, D. Zelazo, D. Mukherjee, and H.-S. Ahn, “Finite-Time Bearing-Only Formation Control via Distributed Global Orientation Estimation,” IEEE Transactions on Control of Network Systems, 6(2):702–712, 2019.
    VanTran2019.pdf DOI: 10.1109/tcns.2018.2873155 VanTran2019.bibtex
  25. S. Zhao and D. Zelazo, “Bearing Rigidity Theory and its Applications for Control and Estimation of Network Systems: Life beyond distance rigidity,” IEEE Control Systems Magazine, 39(2):66–83, 2019.
    Zhao2017_J.pdf DOI: 10.1109/mcs.2018.2888681 Zhao2017_J.bibtex
  26. M. H. Trinh, S. Zhao, Z. Sun, D. Zelazo, B. D. O. Anderson, and H. Ahn, “Bearing-Based Formation Control of A Group of Agents with Leader-First Follower Structure,” IEEE Transactions on Automatic Control, 64(2):598–613, 2019.
    Hoang2016a_J.pdf DOI: 10.1109/tac.2018.2836022 Hoang2016a_J.bibtex
  27. D. Goldenberg, “Cooperative Object Manipulation A Rigidity Approach,” mastersthesis, Technion - Israel Institute of Technology, Aerospace Engineering Department, 2019.
    Goldenberg2019.pdf Goldenberg2019.bibtex
  28. D. Frank, D. Zelazo, and F. Allgöwer, “Bearing-Only Formation Control with Limited Visual Sensing: Two Agent Case,” in 7th IFAC Workshop on Distributed Estimation and Control in Networked System , Groningen, The Netherlands, Sep. 2018.
    Frank2018.pdf DOI: 10.1016/j.ifacol.2018.12.006 Frank2018.bibtex
  29. M. H. Trinh, D. Mukherjee, D. Zelazo, and H.-S. Ahn, “Formations on Directed Cycles with Bearing-Only Measurements,” International Journal of Robust and Nonlinear Control, 28(3):1074–1096, 2018.
    Hoang2016b_J.pdf DOI: 10.1002/rnc.3921 Hoang2016b_J.bibtex
  30. Y. Liu, J. M. Montenbruck, D. Zelazo, M. Odelga, S. Rajappa, H. H. Bülthoff, F. Allgöwer, and A. Zell, “A Distributed Control Approach to Formation Balancing and Maneuvering of Multiple Multirotor UAVs,” IEEE Transactions on Robotics, 34(4):870–882, 2018.
    Liu_IEEETRo2019.pdf DOI: 10.1109/TRO.2018.2853606 Liu_IEEETRo2019.video Liu_IEEETRo2019.bibtex
  31. D. Frank, “Bearing-only Formation Control with Limited View Constraints,” mastersthesis, University of Stuttgart, 2018.
    Frank2019.pdf Frank2019.bibtex
  32. M. H. Trinh, D. Mukherjee, D. Zelazo, and H.-S. Ahn, “Finite-time bearing-only formation control,” in IEEE Conference on Decision and Control, Melbourne, Australia, Dec. 2017.
    Trinh2017c.pdf DOI: 10.1109/cdc.2017.8263876 Trinh2017c.bibtex
  33. S. Zhao, Z. Sun, D. Zelazo, M. H. Trinh, and H.-S. Ahn, “Laman Graphs are Generically Bearing Rigid in Arbitrary Dimensions,” in IEEE Conference on Decision and Control, Melbourne, Australia, Dec. 2017.
    Zhao2017a.pdf DOI: 10.1109/cdc.2017.8264151 Zhao2017a.bibtex
  34. J. M. Montenbruck, D. Zelazo, and F. Allgöwer, “Fekete Points, Formation Control, and the Balancing Problem,” IEEE Transactions on Automatic Control, 62(10):5069–5081, 2017.
    Montenbruck2016a_J.pdf DOI: 10.1109/tac.2017.2679073 Montenbruck2016a_J.bibtex
  35. S. Zhao and D. Zelazo, “Translational and Scaling Formation Maneuver Control via a Bearing-Based Approach,” IEEE Transactions on Control of Network Systems, 4(3):429–438, 2017.
    Zhao2015b_J.pdf DOI: 10.1109/tcns.2015.2507547 Zhao2015b_J.video Zhao2015b_J.bibtex
  36. M. H. Trinh, D. Mukherjee, D. Zelazo, and H.-S. Ahn, “Planar Bearing-only Cyclic Pursuit for Target Capture,” in IFAC World Congress, Toulouse, France, Jul. 2017.
    Trinh2017b.pdf DOI: 10.1016/j.ifacol.2017.08.1759 Trinh2017b.bibtex
  37. D. Mukherjee, M. H. Trinh, D. Zelazo, and H.-S. Ahn, “Bearing-only Cyclic Pursuit in 2-D for Capture of Moving Target,” in 57th Israel Annual Conference on Aerospace Sciences , Tel-Aviv, Israel, Feb. 2017.
    Mukherjee2017a.pdf Mukherjee2017a.slides Mukherjee2017a.bibtex
  38. F. Schiano, A. Franchi, D. Zelazo, and P. R. Giordano, “A Rigidity-Based Decentralized Bearing Formation Controller for Groups of Quadrotor UAVs,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Korea, Sep. 2016.
    Schiano2016a.pdf DOI: 10.1109/iros.2016.7759748 Schiano2016a.video Schiano2016a.bibtex
  39. S. Zhao and D. Zelazo, “Bearing Rigidity and Almost Global Bearing-Only Formation Stabilization,” IEEE Transactions on Automatic Control, 61(6):1255–1268, 2016.
    Zhao2014a_J.pdf DOI: 10.1109/tac.2015.2459191 Zhao2014a_J.video Zhao2014a_J.bibtex
  40. S. Zhao and D. Zelazo, “Localizability and distributed protocols for bearing-based network localization in arbitrary dimensions,” Automatica, 69:334–341, 2016.
    Zhao2015a_J.pdf DOI: 10.1016/j.automatica.2016.03.010 Zhao2015a_J.bibtex
  41. D. Mukherjee, M. H. Trinh, D. Zelazo, and H.-S. Ahn, “Robustness of Heterogeneous Cyclic Pursuit,” in 56th Israel Annual Conference on Aerospace Sciences , Tel-Aviv, Israel, Feb. 2016.
    Mukherjee2016IACAS.pdf Mukherjee2016IACAS.bibtex
  42. O. Rozenheck, “Distance-Constrained Formation Tracking Control,” mastersthesis, Technion - Israel Institute of Technology, Aerospace Engineering Department, 2016.
    Rozenheck2016.pdf Rozenheck2016.bibtex
  43. M. M. Montenbruck, D. Zelazo, and F. Allgöwer, “Retraction Balancing and Formation Control,” in 54th IEEE Conference on Decision and Control, Osaka, Japan, Dec. 2015.
    Montenbruck2015.pdf DOI: 10.1109/cdc.2015.7402784 Montenbruck2015.bibtex
  44. D. Zelazo, P. R. Giordano, and A. Franchi, “Bearing-Only Formation Control Using an SE(2) Rigidity Theory,” in 54th IEEE Conference on Decision and Control, Osaka, Japan, Dec. 2015.
    Zelaxo2015c1.pdf DOI: 10.1109/cdc.2015.7403182 Zelaxo2015c1.bibtex
  45. S. Zhao and D. Zelazo, “Bearing-Based Formation Stabilization with Directed Interaction Topologies,” in 54th IEEE Conference on Decision and Control, Osaka, Japan, Dec. 2015.
    Zhao2015c1.pdf DOI: 10.1109/cdc.2015.7403181 Zhao2015c1.bibtex
  46. S. Zhao and D. Zelazo, “Bearing-Based Formation Maneuvering,” in IEEE International Symposium on Intelligent Control, Sydney, Australia, Sep. 2015.
    Zhao2015c2.pdf DOI: 10.1109/isic.2015.7307285 Zhao2015c2.video Zhao2015c2.bibtex
  47. O. Rozenheck, S. Zhao, and D. Zelazo, “A Proportional-Integral Controller for Distance-Based Formation Tracking,” in European Control Conference, Linz, Austria, Jul. 2015.
    Rozenheck2014b.pdf Rozenheck2014b.slides DOI: 10.1109/ecc.2015.7330781 Rozenheck2014b.bibtex
  48. S. Zhao and D. Zelazo, “Bearing-Based Distributed Control and Estimation of Multi-Agent Systems,” in European Control Conference, Linz, Austria, Jul. 2015.
    Zhao2014a.pdf Zhao2014a.slides DOI: 10.1109/ecc.2015.7330866 Zhao2014a.bibtex
  49. O. Rozenheck, S. Zhao, and D. Zelazo, “Formation Velocity Tracking with Proportional Control,” in 55th Israel Annual Conference on Aerospace Sciences , Haifa, Israel, Feb. 2015.
    Rozenheck2014a.pdf Rozenheck2014a.bibtex
  50. D. Zelazo, A. Franchi, H. H. Bülthoff, and P. Robuffo Giordano, “Decentralized Rigidity Maintenance Control with Range-only Measurements for Multi-Robot Systems,” International Journal of Robotics Research, 34(1):105–128, 2015.
    Zelazo2013a_J.pdf DOI: 10.1177/0278364914546173 Zelazo2013a_J.video Zelazo2013a_J.bibtex
  51. D. Zelazo, A. Franchi, and P. R. Giordano, “Rigidity Theory in SE(2) for Unscaled Relative Position Estimation Using Only Bearing Measurements,” in European Control Conference, Strasbourg, France, Jun. 2014.
    Zelazo2014.pdf Zelazo2014.slides DOI: 10.1109/ECC.2014.6862558 Zelazo2014.bibtex
  52. D. Zelazo, A. Franchi, F. Allgöwer, H. H. Bülthoff, and P. Robuffo Giordano, “Rigidity Maintenance Control for Multi-Robot Systems,” in Proceedings of Robotics: Science and Systems, Sydney, Australia, Jul. 2012.
    Zelazo2012c.pdf DOI: 10.15607/rss.2012.viii.060 Zelazo2012c.bibtex
  53. D. Zelazo and F. Allgöwer, “Growing Optimally Rigid Formations,” in American Control Conference, Montreal, Canada, 2012.
    Zelazo2012.pdf DOI: 10.1109/acc.2012.6315460 Zelazo2012.bibtex
  54. D. Zelazo, A. Rahmani, J. Sandhu, and M. Mesbahi, “Decentralized Formation Control via the Edge Laplacian,” in American Control Conference, Seattle, WA, Jun. 2008.
    Zelazo2008a.pdf DOI: 10.1109/ACC.2008.4586588 Zelazo2008a.bibtex