Passivity and Nonlinear Control

Over the last few decades, many engineering systems have become much more complex, as networked systems and large-scale systems turned common, and “system-of-systems” evolved into a leading design methodology. To address the ever-growing complexity of systems, many researchers suggested various component-level tools that guarantee system-level properties. One important example of such a notion is passivity, which can be informally stated as “energy-based control.” Passivity theory has proven to be a powerful tool across many application domains, primarily due to interconnection preserving properties and connections to performance and stability analysis of nonlinear systems.

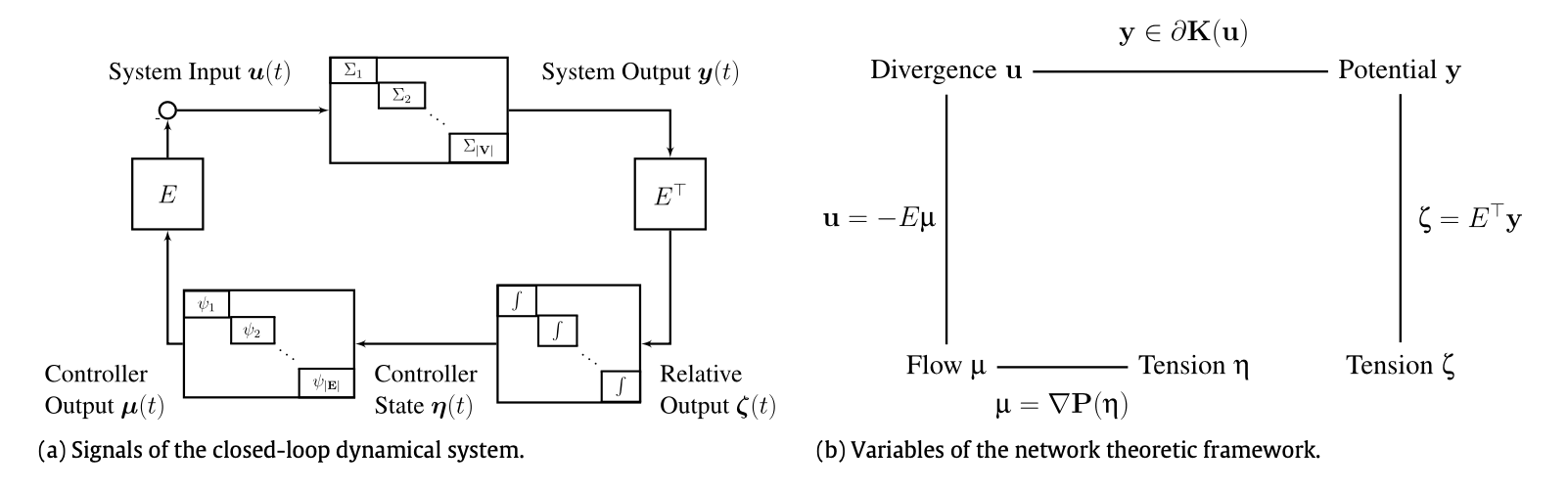
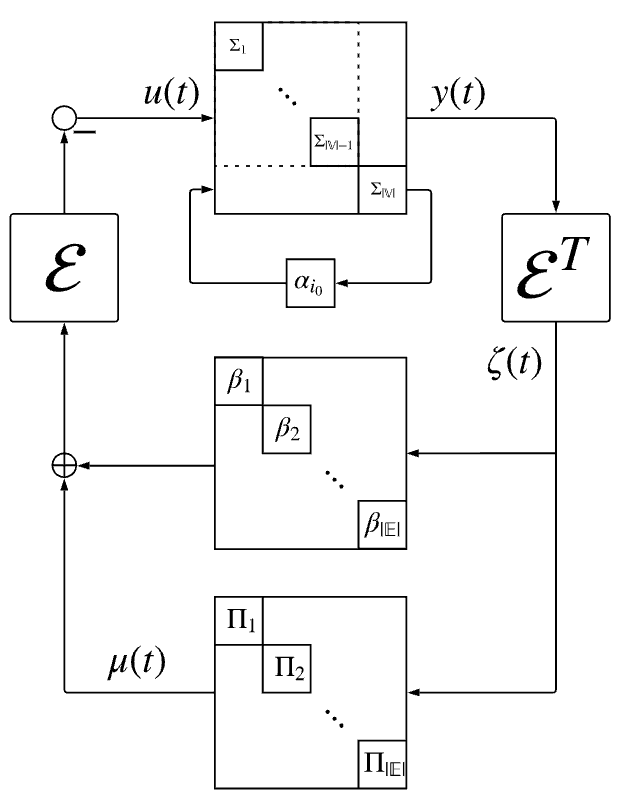
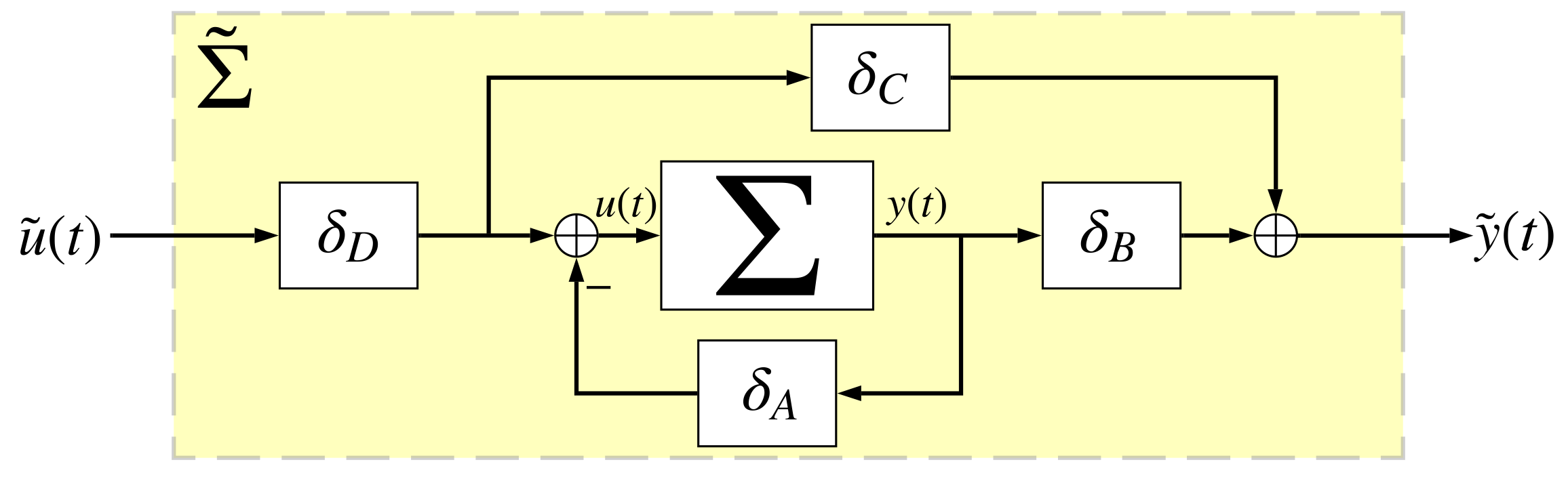
Our research focuses primarily on passivity theory as both an analysis and synthesis tool for networked systems. Our most profound result shows that diffusively coupled networked systems can be analyzed using notions from convex networked optimization theory where passivity serves as the bridge between the dynamical systems world and the optimization world. This work has led to new geometric and optimization based approaches for passivation of passivity-short systems.

Diffusive Networks and Network Optimization Network Passivation Passivation, monotonicity, and convexity

Related Publications:

  1. F. Yue and D. Zelazo, “A Passivity Analysis for Nonlinear Consensus on Digraphs,” in 64th IEEE Conference on Decision and Control, Rio de Janerio, Brazil, Dec. 2025.
    Yue2025_CDC.pdf Yue2025_CDC.slides Yue2025_CDC.bibtex
  2. M. Sharf and D. Zelazo, “A Characterization of Passivizing Input-Output Transformations of Nonlinear MIMO Systems,” IEEE Control Systems Letters, 8:2733–2738, 2024.
    Sharf2024_J.pdf DOI: 10.1109/LCSYS.2024.3513238 Sharf2024_J.bibtex
  3. M. Sharf and D. Zelazo, “A Characterization of All Linear Passivizing Input-Output Transformations of a Passive-Short System: The SISO Case,” IEEE Control Systems Letters, 8:532–537, 2024.
    Sharf2021c_J.pdf Sharf2021c_J.slides DOI: 10.1109/LCSYS.2024.3396616 Sharf2021c_J.bibtex
  4. M. Sharf, A. Jain, and D. Zelazo, “Geometric Method for Passivation and Cooperative Control of Equilibrium-Independent Passive-Short Systems,” IEEE Transactions on Automatic Control, 66(12):5877–5892, 2021.
    Sharf2019c_J.pdf DOI: 10.1109/tac.2020.3043390 Sharf2019c_J.bibtex
  5. M. Sharf, “Network Optimization Methods in Passivity-Based Cooperative Control,” phdthesis, Technion - Israel Institute of Technology, Aerospace Engineering Department, 2020.
    Sharf2020.pdf Sharf2020.bibtex
  6. M. Sharf and D. Zelazo, “Analysis and Synthesis of MIMO Multi-Agent Systems Using Network Optimization,” IEEE Transactions on Automatic Control, 64(11):1558–2523, 2019.
    Sharf2017b_J.pdf DOI: 10.1109/tac.2019.2908258 Sharf2017b_J.bibtex
  7. M. Sharf and D. Zelazo, “Symmetry-Induced Clustering in Multi-Agent Systems using Network Optimization and Passivity,” in 27th Mediterranean Conference on Control and Automation, Akko, Israel, Jul. 2019.
    Sharf2019a.pdf Sharf2019a.slides DOI: 10.1109/med.2019.8798507 Sharf2019a.bibtex
  8. M. Sharf and D. Zelazo, “Network Feedback Passivation of Passivity-Short Multi-Agent Systems,” IEEE Control Systems Letters, 3(3):607–612, 2019.
    Sharf2019a_J.pdf Sharf2019a_J.slides DOI: 10.1109/lcsys.2019.2914128 Sharf2019a_J.bibtex
  9. M. Sharf and D. Zelazo, “Network Identification: A Passivity and Network Optimization Approach,” in IEEE Conference on Decision and Control, Miami, Florida, Dec. 2018.
    Sharf2018a.pdf DOI: 10.1109/cdc.2018.8619059 Sharf2018a.bibtex
  10. A. Jain, M. Sharf, and D. Zelazo, “Regularization and Feedback Passivation in Cooperative Control of Passivity-Short Systems: A Network Optimization Perspective,” IEEE Control Systems Letters, 2(4):731–736, 2018.
    Jain2018a_J.pdf DOI: 10.1109/lcsys.2018.2847738 Jain2018a_J.bibtex
  11. M. Sharf and D. Zelazo, “A Network Optimization Approach to Cooperative Control Synthesis,” IEEE Control Systems Letters, 1(1):86–91, 2017.
    Sharf2017a_J.pdf DOI: 10.1109/lcsys.2017.2706948 Sharf2017a_J.bibtex
  12. M. Bürger, D. Zelazo, and F. Allgöwer, “Duality and network theory in passivity-based cooperative control,” Automatica, 50(8):2051–2061, 2014.
    Burger2014_J.pdf DOI: 10.1016/j.automatica.2014.06.002 Burger2014_J.bibtex
  13. M. Bürger, D. Zelazo, and F. Allgöwer, “On the Steady-State Inverse-Optimality of Passivity-Based Cooperative Control,” in 4th IFAC Workshop on Distributed Estimation and Control in Networked System, Koblenz, Germany, Sep. 2013.
    Mathias2013.pdf DOI: 10.3182/20130925-2-DE-4044.00004 Mathias2013.bibtex
  14. D. Zelazo and M. Mesbahi, “Edge Agreement: Graph-Theoretic Performance Bounds and Passivity Analysis,” IEEE Transactions on Automatic Control, 56(3):544–555, 2011.
    Zelazo2009b_J.pdf DOI: 10.1109/TAC.2010.2056730 Zelazo2009b_J.bibtex